LOST IN SPACE

sun
planets
spaceship
estimated spaceship position
sample particles (white dots)
On an intergalactic mission, our spaceship traveled through a wormhole to survey a distant solar system. On the return trip home, the wormhole dropped us in an unknown location around the home sun. The goal of this project was to implement a particle filter to localize our spaceship in the solar system then send messages back to Earth communicating our location.
Duration
jan 2023
Skills
python, particle filter, localization
Problem Setup
We have a model of the solar system (position, velocity, and masses) of the planets and sun. We have a gravimeter which is a sensor that measures the gravitational pull of planets as felt by the spaceship. Using this information we must estimate the position (x, y) of our spaceship in the solar system.
Proposed Solution
An ideal solution to this problem is to implement a particle filter. Particle filters are commonly used for object localization, for both tracking and SLAM (simultaneous localization and mapping). This sample-efficient search technique estimates the likelihood of a state across many locations. The challenges in this problem include:
- Noisy measurements from the gavimeter
- Nonlinear dynamics (gravity follows and inverse-square law)
\[ v = \left| \sum_{p=1}^{n} \frac{G M_p}{r_p^2} \right| \]
\(V\) is the gravity magnitude
\(n\) is the number of planets
\(G\) is the gravitational constant
\(M_p\) is the mass of the planet
\(r_p\) is the vector from the spaceship to the planet
The particle filter formulation can handle both of these challenges. Other localization techniques are possible, but not as well suited for this problem. For example, a Kalman filter relies on linear dynamics. An extended Kalman filter can be used but requires linearizing the dynamics model which may produce inaccurate results for highly nonlinear systems.
Particle Filter Formulation
Initialization
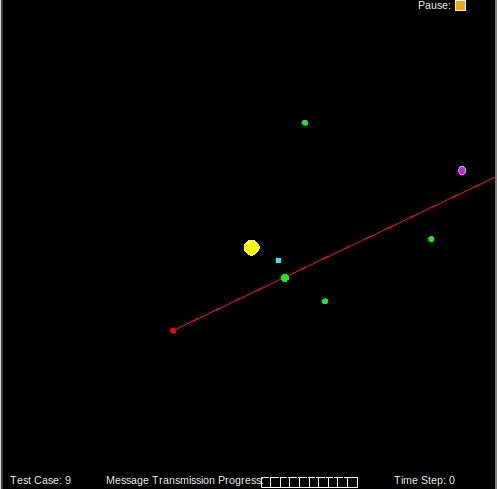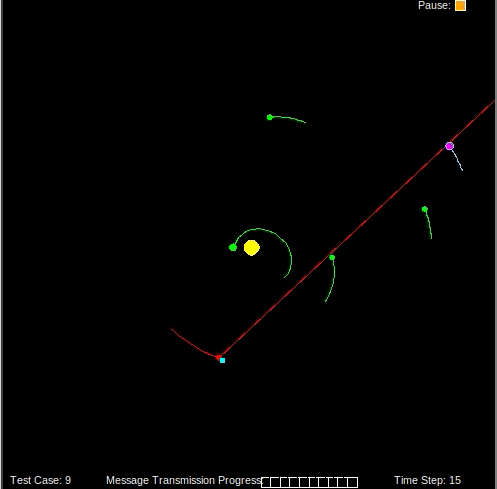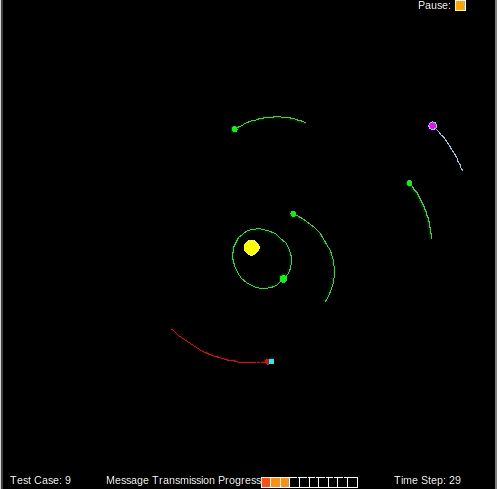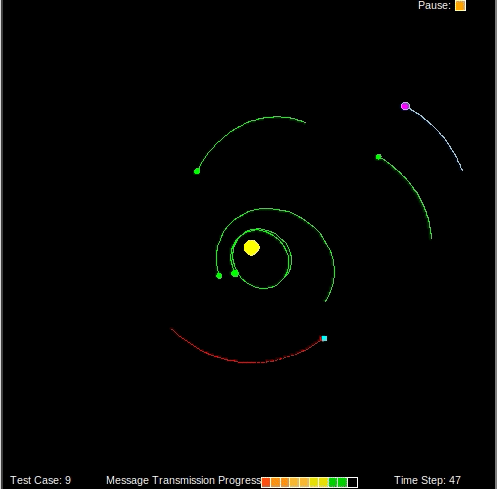
To initialize the filter, we randomly sample N particles representing guesses of the spaceship’s location.
Prediction
For each particle, we must compute the force of gravity given the model of the solar system.
Weight Update
Next, we compute the likelihood of each particle. A high likelihood means the particle’s position is likely to be the spaceship’s position.
\[ F_i = ma_i \]
\[ a_i = \left| \sum_{p=1}^{n} \frac{G M_p (r_p - r_i)}{|r_p - r_i|^3} \right| \]
\[ w_i = \exp\left(-\frac{F_{\text{gravimeter}} - F_i}{σ^2}\right) \]
\(F_i\) is the force of gravity on the particle estimating the spaceship
\(m\) is the mass of the spaceship
\(a_i\) is the acceleration of the particle
\(n\) is the number of planets
\(G\) is the gravitational constant
\(M_p\) is the mass of the planet
\(r_p\) is the position of the planet
\(r_i\) is the position of the particle
\(σ\) is a tunable noise parameter
\(w_i\) is the particle's weight
Resample
Given the weight of each particle, we can discard unlikely particles and resample likely particles to converge on an accurate estimate of the spaceship’s location.
Iterate
We repeat the prediction, weight update and resampling steps as new measurements from the gavimeter come in.
Localize the Spaceship
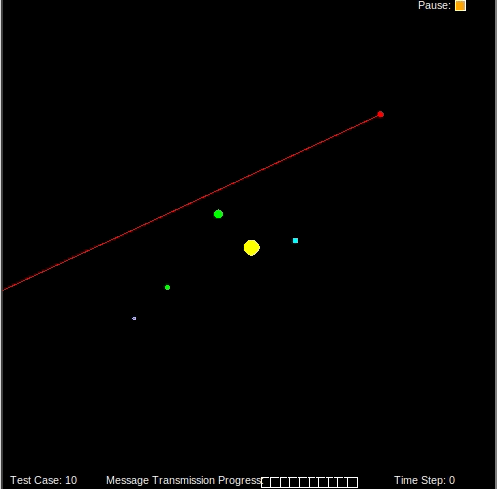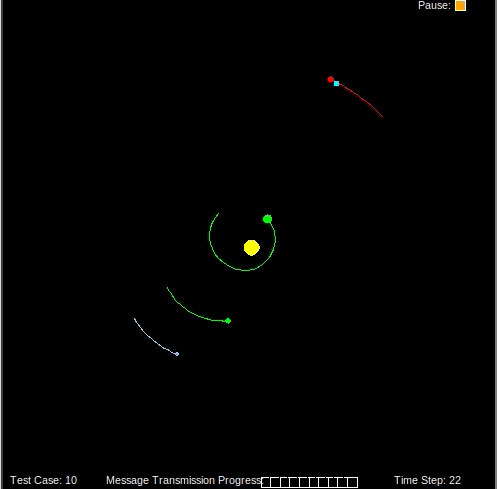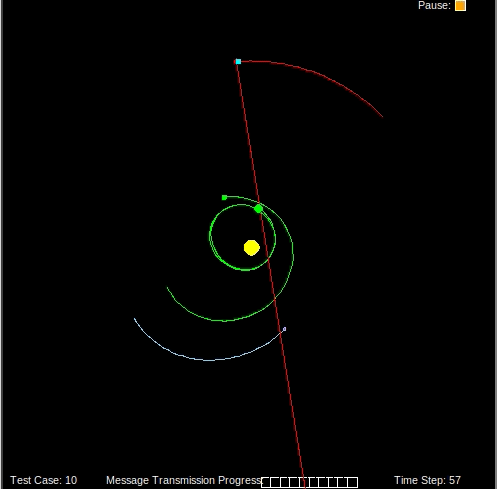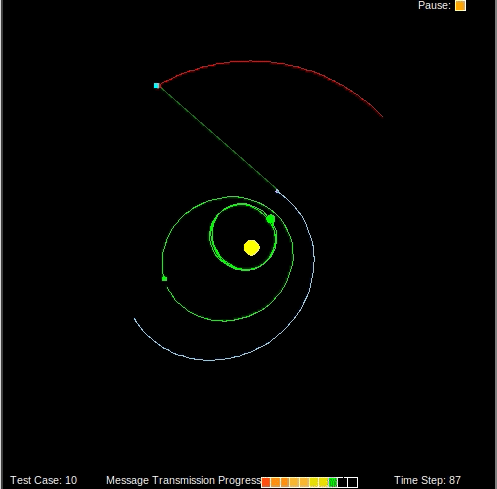
When the filter converges on a solution, there will be many particles around the ground truth location of the spaceship. By computing a weighted average of the particles we can get a good estimate of the spaceship’s location.
Send Messages Home
Once we have a good estimate of the spaceship’s location, sending messages home should be easy given that we already have a model of the solar system containing Earth’s location. We simply find the angle of the vector between the spaceship and Earth and point our radio emitter in that direction.
Results